When it comes to IT, I always try to make something helpful for my Team just not copying and pasting the stuff from the internet. So, I decided that rather than just writing some examples of matrices let's do some more technical and researched based stuff and focus on one thing.
Now, I Decided Let's Take Cryptography First
But The Question Is, Which Algorithm Should We Go For? I knew that taking many or let's just different algorithms gonna make things glitcher (Idk even this word exists) and that nobody wants.
Then, I thought let's consider an algorithm that has some certain key features just like -
- Well Known And Community Supported Algorithm
- Which Provides Military Grade Security
- Way Faster And Symmetric Encryption
- Something Which Is Industry Standard
- And, Never Have Been Broken Till Now
Ye Indeed, the only encryption that satisfies our requirement is AES (Advanced Encryption Standard).
So Ladies And Gentleman Please Welcome Widely Regarded, Most Secure Symmetric Key Encryption Cipher Yet Invented, A Cipher Which Is "1000 Times Faster” Than Asymmetric Ones, Battle-Tested In A Way That No Other Algorithm Have Never Been, Brute Forced Secured In A Way That Even Worlds Most Powerful Computer May Would Take Some Quadrillion Years To Break It, And Even Most CPU Manufacturers Have Now Integrated This Instruction Set Into Their Processors Which Improves The Resistance Towards Side-Channel Attacks.
So, That Cryptographic Encryption Is... Advanced Encryption Standard
And hey, if the US government thinks AES is the best cipher to protect its "secure” data, who’s arguing?
Matrix Application In AES-128
It’s time to hop over to the AES-128 bit encryption. AES is based on SP Network (Substitution-Permutation Network). So, this will be like replacing and shuffling bits here and there.
So, Let’s Build The Base
AES is a block cipher that means any data entered into AES will fragment into blocks. And the block size depends upon your algorithm selection. Here is 128 Bit which is 16 bytes which is equal to 4 words
Text To Encrypt
👇
┌ ----- ┐ ┌ ----- ┐ ┌ ----- ┐ ┌ ----- ┐
└ ----- ┘ └ ----- ┘ └ ----- ┘ └ ----- ┘
And, now AES takes each block (of 128 Bits) then encrypt them one by one. But Question Is How And Where Is Matrix? Ya Okay, Let's Meet Your First Matrix.
As I explained, one block will be input as data. But in which format do you know? Yes, if you guessed Matrix. Each block of 16 bytes or 128 bits will be arranged in a 4 x 4 matrix.
┌ -- ┐┌ -- ┐┌ -- ┐┌ -- ┐
└ -- ┘└ -- ┘└ -- ┘└ -- ┘
┌ -- ┐┌ -- ┐┌ -- ┐┌ -- ┐
└ -- ┘└ -- ┘└ -- ┘└ -- ┘
┌ -- ┐┌ -- ┐┌ -- ┐┌ -- ┐
└ -- ┘└ -- ┘└ -- ┘└ -- ┘
┌ -- ┐┌ -- ┐┌ -- ┐┌ -- ┐
└ -- ┘└ -- ┘└ -- ┘└ -- ┘
Matrix Of 16 Bytes Of Plaintext Block
It's Time To Cuddle With Key
As you may know, Symmetric encryption requires a Key to encrypt or decrypt the data. The Key size would be 128-Bit because you have selected AES 128-Bit Encryption but, you are not restricted here. We can choose 192 or 256 key lengths as well. The below table will provide you with some references.
| Encryption |
Key Size |
Block Size |
Rounds |
| AES 128-Bit |
128 Bit |
128 Bit |
10 |
| AES 192-Bit |
192 Bit |
128 Bit |
12 |
| AES 256-Bit |
256 Bit |
128 Bit |
14 |
"All Values Of Block Size Column Is Same Which Show AES Is A Fixed Block Encryption"
So Again, What will be the format of Key as an input? If you guessed right, It’s matrix format. A 128-Bit or 16 Bytes or 4 Words matrix will be represented 128-Bit Key just like below-
| k_0 |
k_4 |
k_8 |
k_12 |
| k_1 |
k_5 |
k_9 |
k_13 |
| k_2 |
k_6 |
k_10 |
k_14 |
| k_3 |
k_7 |
k_11 |
k_15 |
|
👉👉 |
| w_0 |
w_1 |
w_2 |
w_3 |
w_4 |
… |
… |
w_43 |
|
After arranging our Key in the matrix, What we have done in another 1-d matrix is called Key Expansion which means I have expanded our 128 bit Key into 44 Words.
"Hey! How is going on? Don’t Forget Now We Have 3 Matrices"
Game On Level Upgraded
Now you have acquired knowledge to move forward and are ready to see your first flow chart where all your hard work will pay off.
AddRoundKey is our first function that XOR the Plaintext Matrix of 128 bits or first block with 4 Words or 128 Bits Key Cipher Matrix which we have created in the above section It’s Time To Cuddle With Key. Now it is time to feed data (matrix) generated by the AddRoundKey function to rounds (In This Case, 10 Rounds)
Wohoo, Everything is matrix
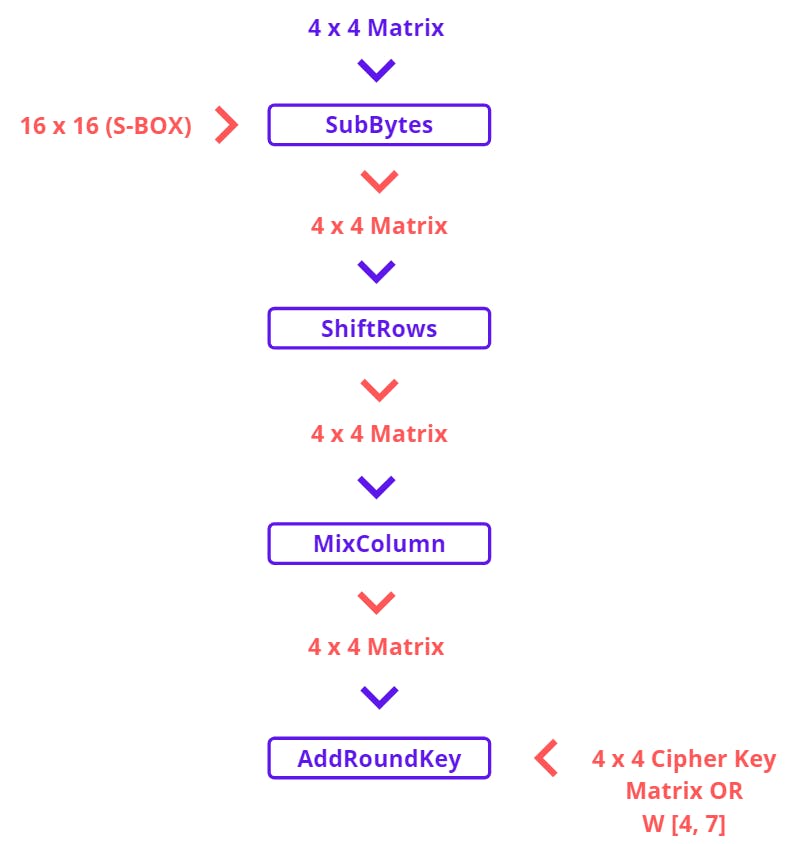
A Round contains several mathematical steps and one round may look like this -
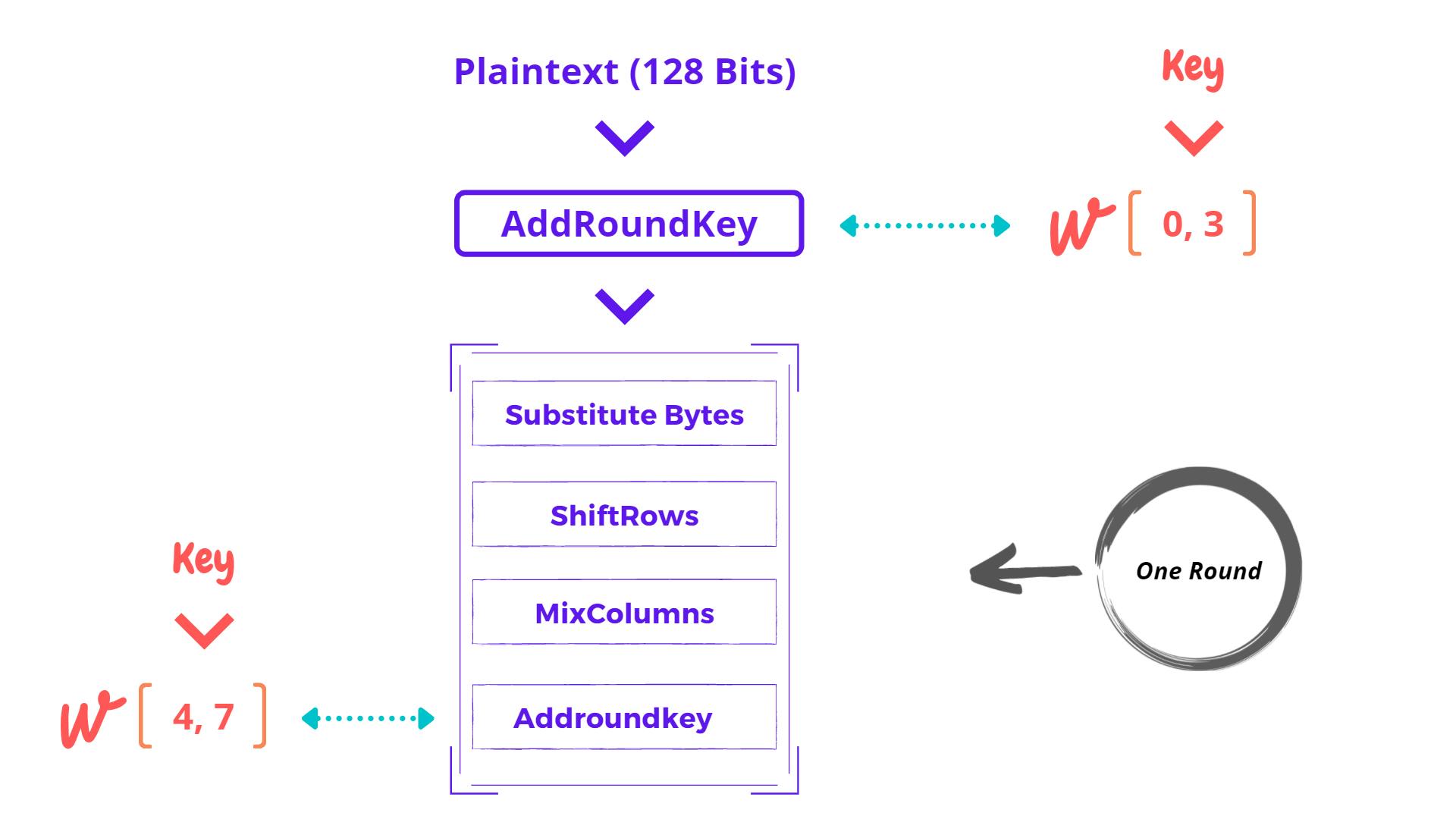
Each round has 4 functions. Let’s discuss one by one but before this point, note that our all intermediate results will gonna stored in 16 bytes of a matrix which is known as State Array.
For example, AddRoundKey will give an output of 128 Bits matrix and that matrix is sent to first round function SubBytes. This function will again generate an output. The output generated by every other function will be stored in a Matrix called State Array. Then, we can also say State Array holds the results of the current process. So, the next function can access State Array.
| S 0,0 |
S 0, 1 |
S 0, 2 |
S 0, 3 |
| S 1,0 |
S 1, 1 |
S 1, 2 |
S 1, 3 |
| S 2,0 |
S 2, 1 |
S 2, 2 |
S 2, 3 |
| S 3,0 |
S 3, 1 |
S 3, 2 |
S 3, 3 |
- One Column Is Equal To 1 Word (As Above Matrices)
- First Number Represents Byte And Second Number Represents Word
- Pronunciation Of State Matrix0th Byte Of 0th Word
- 0th Byte Of 0th Word
- 1st Byte Of 0th Word
- 2nd Byte Of 0th Word
- ……
- ……
- 2nd Byte Of 3rd Word
- 3rd Byte Of 3 Word
if you didn’t understand, You can take it as “Output Generated By Each Function Gonna Store In A Matrix Which Is Called State Matrix And This State Matrix Can Also Be A Input For Next Function”
Plaintext Array -> AddRoundKey -> (State Array) -> SubBytes -> (State Array) -> ShiftRows …
Hmm… I know, I’m emphasizing this so much even it is very simple but at last time a different analogy for Programmers or IT Ninjas. “State Array Is A Global Variable Which Can Be Accessed And Overwrite By Any Function”
woohoo, enough that’s the end of state matrix or array (no matter)
What Happens In One Round?
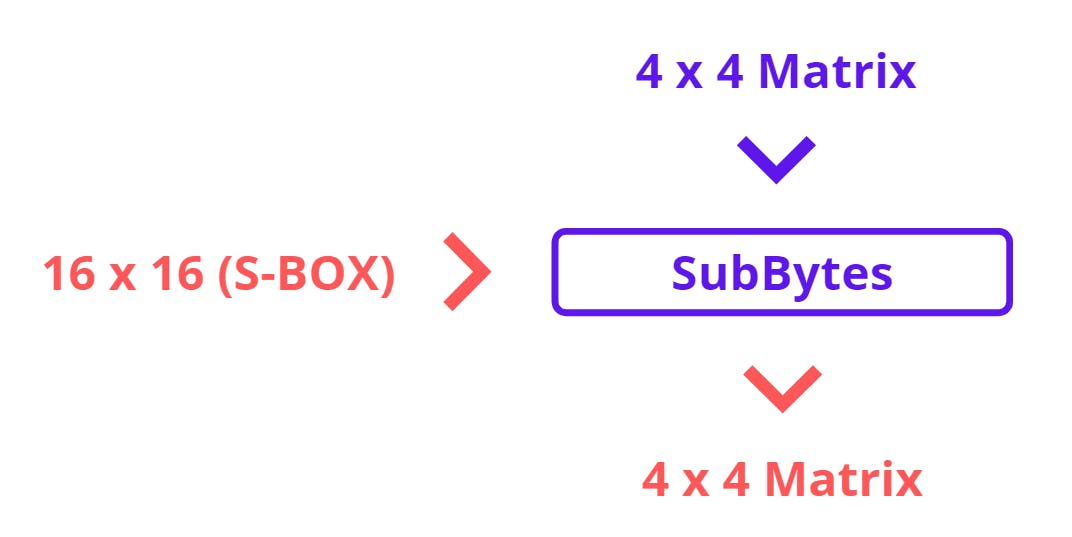
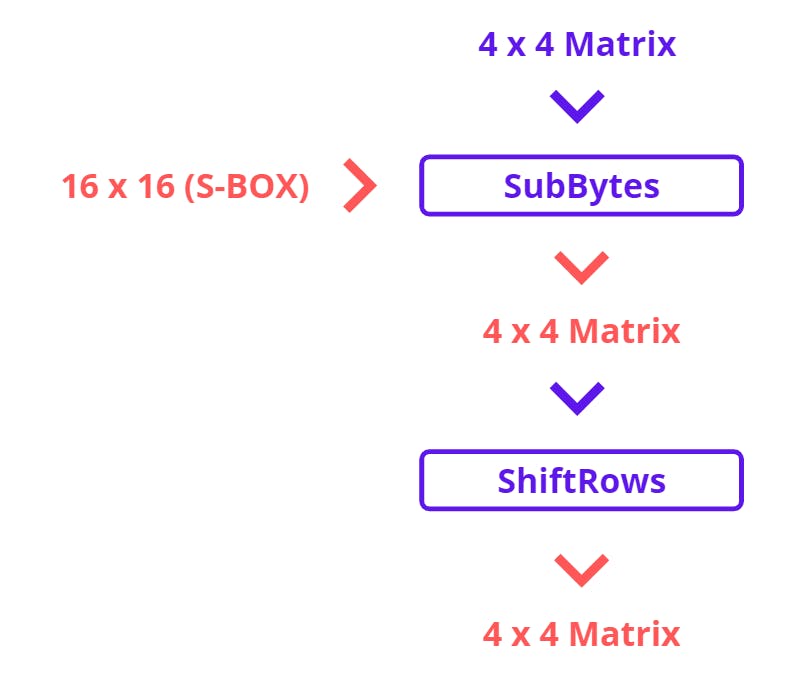
Substitute Bytes takes the input of 4 x 4 State Matrix and 16 x 16 AES S Table also known as S-BOX. S-BOX is a fixed table that helps to substitute 16 bytes or 128 Bits or 4 Words of state matrix (Just for revision) and generates a 4 x 4 matrix. And this will become a State Matrix for the next function.
Shiftrows will shift the 1 byte (one cell of a matrix) towards the left position according to row index.
| Index |
|
|
|
|
| 0 |
S 0,0 |
S 0,1 |
S 0,2 |
S 0,3 |
| 1 |
S 1,0 |
S 1,1 |
S 1,2 |
S 1,3 |
| 2 |
S 2,0 |
S 2,1 |
S 2,2 |
S 2,3 |
| 3 |
S 3,0 |
S 3,1 |
S 3,2 |
S 3,3 |
|
👉👉 |
| S 0,0 |
S 0, 1 |
S 0, 2 |
S 0, 3 |
| S 1,1 |
S 1, 2 |
S 1, 3 |
S 1, 0 |
| S 2,2 |
S 2, 3 |
S 2, 0 |
S 2, 1 |
| S 3,3 |
S 3, 0 |
S 3, 1 |
S 3, 2 |
|
So, as we can see that now, each rows byte shifts left concerning the row index. Except for the first row because its index is zero and now we have a new matrix of 16 bytes with shifted rows.
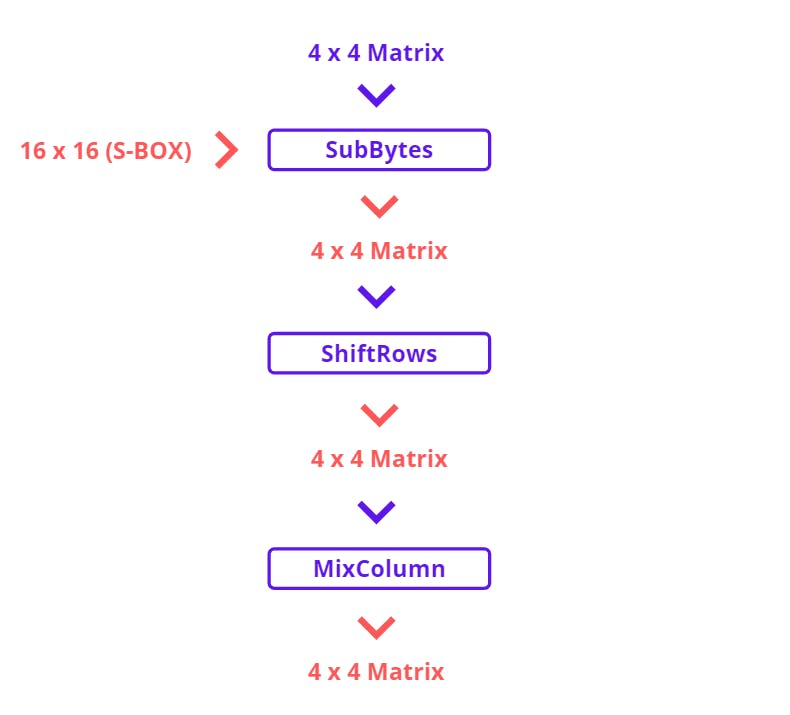
MixColumn, as expected, takes two inputs one is 4 x 4 state matrix and another 4 x 4 fixed matrix (shown below)
| 2 |
3 |
1 |
1 |
| 1 |
2 |
3 |
1 |
| 1 |
1 |
2 |
3 |
| 3 |
1 |
1 |
2 |
|
👈 4 x 4 Fixed Array |
| S 0,0 |
S 0, 1 |
S 0, 2 |
S 0, 3 |
| S 1,0 |
S 1, 1 |
S 1, 2 |
S 1, 3 |
| S 2,0 |
S 2, 1 |
S 2, 2 |
S 2, 3 |
| S 3,0 |
S 3, 1 |
S 3, 2 |
S 3, 3 |
|
👈 4 x 4 State Array |
So, this is how the complex begins. First, we would take each column of state matrix or array one by one and then multiply with Fixed Matrix. After that, as expected! the result will be another new matrix consisting of 16 new bytes or a 4 x 4 matrix (some visuals below how this happens)
|
|
X |
| 2 |
3 |
1 |
1 |
| 1 |
2 |
3 |
1 |
| 1 |
1 |
2 |
3 |
| 3 |
1 |
1 |
2 |
|
= |
| S' 0,0 |
| S' 1,0 |
| S' 2,0 |
| S' 3,0 |
|
|
|
X |
| 2 |
3 |
1 |
1 |
| 1 |
2 |
3 |
1 |
| 1 |
1 |
2 |
3 |
| 3 |
1 |
1 |
2 |
|
= |
| S' 0,1 |
| S' 1,1 |
| S' 2,1 |
| S' 3,1 |
|
|
|
X |
| 2 |
3 |
1 |
1 |
| 1 |
2 |
3 |
1 |
| 1 |
1 |
2 |
3 |
| 3 |
1 |
1 |
2 |
|
= |
| S' 0,2 |
| S' 1,2 |
| S' 2,2 |
| S' 3,2 |
|
|
|
X |
| 2 |
3 |
1 |
1 |
| 1 |
2 |
3 |
1 |
| 1 |
1 |
2 |
3 |
| 3 |
1 |
1 |
2 |
|
= |
| S' 0,3 |
| S' 1,3 |
| S' 2,3 |
| S' 3,3 |
|
Let's merge them all together and generate a new state array
| S' 0,0 |
| S' 1,0 |
| S' 2,0 |
| S' 3,0 |
|
| S' 0,1 |
| S' 1,1 |
| S' 2,1 |
| S' 3,1 |
|
| S' 0,2 |
| S' 1,2 |
| S' 2,2 |
| S' 3,2 |
|
| S' 0,3 |
| S' 1,3 |
| S' 2,3 |
| S' 3,3 |
|
= |
| S 0,0 |
S 0, 1 |
S 0, 2 |
S 0, 3 |
| S 1,0 |
S 1, 1 |
S 1, 2 |
S 1, 3 |
| S 2,0 |
S 2, 1 |
S 2, 2 |
S 2, 3 |
| S 3,0 |
S 3, 1 |
S 3, 2 |
S 3, 3 |
|
Now AddRoundKey function is again encountered here that we also discussed above. So, this function accepts two inputs one is 4 x 4 state matrix and 4 Word from Key Expansion then we will XOR both of them. This is the last function of each round.
That Set, This whole process was just for 1 round. We need to do the same process again till round 9th the only difference for round 10th is last round doesn’t contain the MixColumn function that will directly jump from ShiftRows To AddRoundKey in the last round and that will generate your Cipher Text.
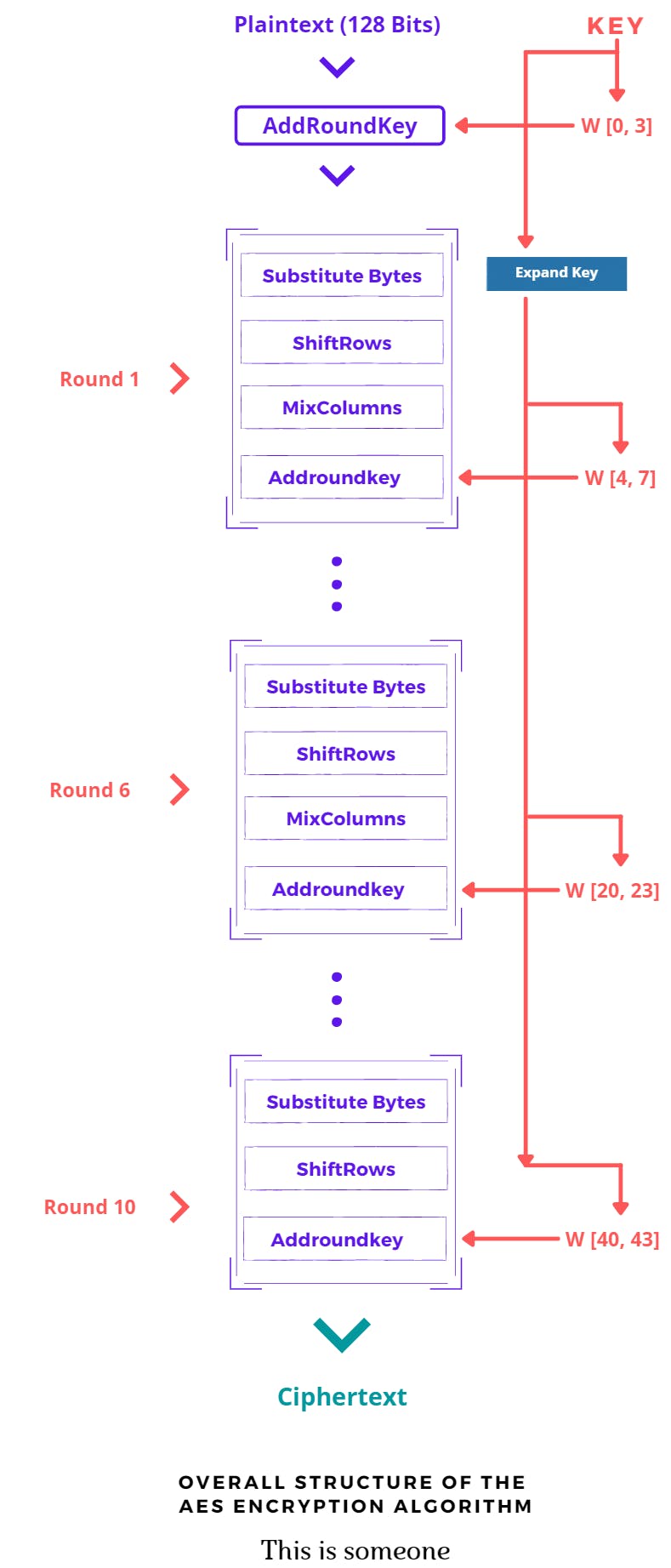
Note: Don’t forget last 10th round in this case doesn’t consist MixColumn function
Hint: Just Reverse The Algorithm 👉 (unSeCrEt)
Real-world Applications of Matrices
(Cheated From Internet)
Encryption
In encryption, we use it to scramble data for security purposes to encode and to decode this data we need matrices. There is a key that helps encode and decode data which is generated by matrices.
Games especially 3D (SHOULD WE COVER THIS IN NEXT REPORT) use it to alter the object, in 3d space. They use the 3d matrix to 2d matrix to convert it into the different objects as per requirement.
Animation: It can help make animations more precise and perfect.
Physics: Matrices are applied in the study of electrical circuits, quantum mechanics, and optics. It helps in the calculation of battery power outputs, resistor conversion of electrical energy into another useful energy.
Conclusion
That was our journey about how Matrices help us in particular Cryptography. There was a lot to say but then this will end up like a Security Research Paper. As you have noticed, not only data but each and every bit flowing in this algo was in form of a Matrix. And Ya.., I Tried To Make It In Fun Way.
Now, Should I Say Everything Is Matrix?
No… Noway, If You Know Something Doesn’t Mean That Is Everything.
